The really powerful thing you can do with a decimal number is to get rid of it: Use the yellow APRX function. APRX is short for 'Approximate', and what it does is generate in F2 an efficient stacked version of the decimal number in F1intD. (By "efficient" we mean a stack with small numerator and denominator whose decimal accurately matches the given decimal.)
Decimal-to-Stack conversion is a surprisingly subtle task. For example, the standard conversion of the famous number e, accurate to 8 digits, is 2 + 7,182,818/10,000,000. To 4 digits it is easily approximated by 2 + 718/1,000. But 2 + 719/1,001 which looks almost the same, is way more accurate (7 digits—off by only 1 in the 8th digit). You don't figure out stuff like that by a quick calculation in your head.
 |
00 copies Fdec to F1intD: Internally, APRX generates five different efficient decimal-to-stack conversions then selects the best of the five and presents it to you in Fraction F2. This can sometimes be very handy. To get Fig. APRX1, we made F1intD be the decimal fraction 12.543 and ytapped APRX.  Figure APRX1 Summary of all five methods is shown. As you can see, the result (given in Fraction F2) was excellent. The standard mixed form — listed fourth in the ranking — is 12+543/1000, whose denominator is much larger than that of the 12+19/35 that Frrraction's APRX Method 3 found.
This  links to a page that explains the standard conversion, APRX's "Method 0 std exact". Calling it "9 Recurring", Math is Fun also includes a Special Note explaining part of the APRX "Method 1 repeat pattern".
|
background
CF stands for "Composite Functions", a term meant to distinguish them from Frrraction's basic built-ins. The CF facility provides a way for users to automate their fraction calculations by writing programs—sequences of Frrraction keycodes—that can be performed whenever they yTap the CF key. It also provides a way to essentially enlarge the number of useable keys beyond the sixteen permitted by the limited space on iPhone screens.
To use CFs, you Edit a Note to include one or more "CF Brackets", which are matched pairs of braces enclosing sequences that define the functions. There are three kinds of Composite Function: Egyptian Fractions, Continued Fractions, and Program Functions. Within a Note, their brackets look like this:
| CF | Bracket | entries |
|---|---|---|
| Egyptian Fraction | integer denominators | |
| Continued Fraction | integer quotients | |
| Program Function | action keywords |
Classic Fractions—Egyptian Fractions and Continued Fractions—are similar to each other in style, and simpler to use than Program Functions, so we discuss them in the next section. Following that, we go into the details of Program Functions.
There are two kinds of classic fractions: Continued Fractions and Egyptian Fractions. Continued Fractions are cool for a number of uses, including the secret codes my Grandson Galen and I are doing. Egyptian Fractions built the pyramids 4000 years ago. They're still good for divvying things among people, but aren't useful for much else any more.
An example Continued Fraction is:
5 + 1 / (4 + 1/ (3 + 1/ 2 )).
In normal notation, this continued fraction would be written something like this:
1
5 + ——————————————
1
4 + —————————
1
3 + ————
2
Classic Fractions are awkward to type, so Frrraction abbreviates them with a widely used shorthand bracket notation: Square brackets formed with the square braces [ and ] enclose Continued Fractions, and curly brackets formed with the curly braces { and } enclose Egyptian Fractions — look closely, those Egyptian curly braces are not the normal smooth parentheses.
The integer part of the fraction immediately follows the opening brace, and is followed by a semicolon.
If there is no integer part then the first entry within the bracket is 0 followed by a semicolon, viz. [0;a,b].
If the fraction has the mixed form a+0/1 i.e. there is nothing but an integer part then the bracket is simply [a;]. Don't omit the semicolon, though—without it, CF doesn't even recognize <[a] as a continued fraction command.
After the semicolon, the quotients (fraction parts) follow in order, each followed by a comma — although the final comma before the closing brace is usually omitted. For example, the continued fractions [5;4,3,2] and [5;4,3,2,] have integer part 5 and fraction parts 4, 3, and 2 and they equal 157/30.
YTapping Frrraction's CF key performs any of several tasks, depending upon what brackets you've put into frrrNotes.
You don't really need the CF function in order to work with classic fractions, of course. You can use normal Frrraction arithmetic or just do the work by hand. Of course, you could wear itchy old hair shirts instead of soft cotton, too.
For example, to convert [5;4,3,2] into an ordinary stacked fraction, the following steps (working from back to front) would do it:
and there you have it: [5;4,3,2] is 5+7/30, or 157/30. (Frrraction's M|P function will convert the mixed fraction 5+7/30 into the pure fraction 157/30 if you don't want to do that chore by hand.)
Here's a procedure to go the other way — convert 157/30 into a continued fraction (writing the bracket down by hand as you go, I suppose):
| Keywords | action |
|---|---|
F2num F2den F2int |
make the named fraction cell become active |
F2 |
make the named fraction—specifically, the cellmate of the present cell—become active |
| clear the active fraction cell to zero | |
| backspace-delete digits from the active fraction cell | |
0 |
like tapping the named digit key, even if preceded by Y RCL or Y STO |
| doubleTap 0 (decimal fraction to F1int retasked as F1dec) | |
| these act like tapping the math op keys You can use + – * / if you prefer. Unfortunately, Apple omitted ÷ from the iThing keyboard, so / must serve for div. | |
| this acts like tapping the yellow key, and must precede each yellow function | |
DUP MAX pMAX nMAX ONE GCD |
these represent the yellowFunctions shared by the digit keys. |
| these represent the yellowFunctions shared by the math-op keys | |
| A CF program loop is an @-group: A group of brackets each with a prefix-@, and the last one with a single inside-@. THE inside-@ can be placed anywhere in the last member of an @-group of cf-brackets (putting it near the bracket's closing double-brace makes it nicely visible when you are developing the program). An @-group behaves this way: When the cf bracket with the inside-@ finishes running, the cf facility searches the entire frrrNote from the top to the position of the inside-@ and replaces all instances of the pattern @{{ by @<{{. What this does is to re-enables all members of the @-group, permitting the run-cycle to start over again with the top member of the group the next time CF is tapped—without the user being required to use EDIT to manually re-enable the group members. The @-command has no effect on cf brackets other than those whose opening is currently tagged by @{{, viz. un-enabled cf brackets the user has designated for inclusion in the cyclic @-group. | |
FILE |
these are INTENTIONALLY OMITTED from the CF-function lexicon |
Key idea
|
Try it. Use the editor to change the above example to give it two enablers, so it looks like this: The function (assuming it's the enabled CF closest to the top of frrrNote) can then be executed twice before becoming dormant. You can confirm the operation: Put - 21/33 into fraction F1 then do Y STO 5 to put it into register R5 as a test value; run CF twice; then activate fraction F2 and tap the key-sequence Y RCL 5. At that point, F2 will also contain the same value as F1: 15/11. If you'd like to execute it repeatedly, without having to use EDIT to add more enablers whenever it runs out of them, use the @-loop facility like this: Now the bracket will run every time you tap CF. If you'd like automatic one-time initialization to be done by the first CF-tap, with subsequent CF-taps running the @-loop, you can add something like this before the @-loop in the frrrNote: Now the first time you run CF the initialization will run; that uses up its single <enabler so, the next time you run CF it will be the @-loop that runs, using up that bracket's single <enabler. When the cf system encounters the bracket's inside-@ it will restore the depleted <enabler, setting things up so the next run of CF will re-run the @-loop again. This will repeat as often as you tap CF. |
Key idea
and Down- 
navigator buttons try to position the insertion cursor at the enabler-positions of the various CF functions—that's what the squigglies at the bottom of the keys are meant to remind you—so enablers can be easily replenished.
Some CF Program functions aren't available on Frrraction's keyboard due to lack of space. One of the best of the missing functions is hp(. 'hp' stands for ''high precision'. What it provides is a 64-bit integer-and-floatingPoint decimal programmable calculator for those times when Frrraction's 32-bit integers need some help. It uses RPN (Reverse Polish Notation), automatically accessing a five-deep XYZTU number-stack as needed.
A typical reason to appreciate hp( arises when you compute a high accuracy square root of a fraction. To confirm the result you'd like to multiply the result by itself—doing something like Y DUP ×. But if the numerator or denominator of the putative result exceeds 46,340 (the integer square root of pMAX) the multiplication will cause overflow. Here's where hp( can come to the rescue, because multiplication of two 32-bit numbers cannot overflow in 64-bit arithmetic.
Among its other resources, hp( gives separate access to each of Frrraction's integer cells, individually and in combination, allowing manipulation beyond conventional fraction paradigms. An easy example: Want to give F2's stack a non-unit gcd, to exercise the yellow GCD key? Use hp( to multiply each of F2num and F2den by the desired common divisor. If F2=2+4/5 you can convert it that way into 2+12/15. As with many other hp( operations there's no other way to do it. Putting 0+3/3 into F1 and multiplying does not have the intended effect.
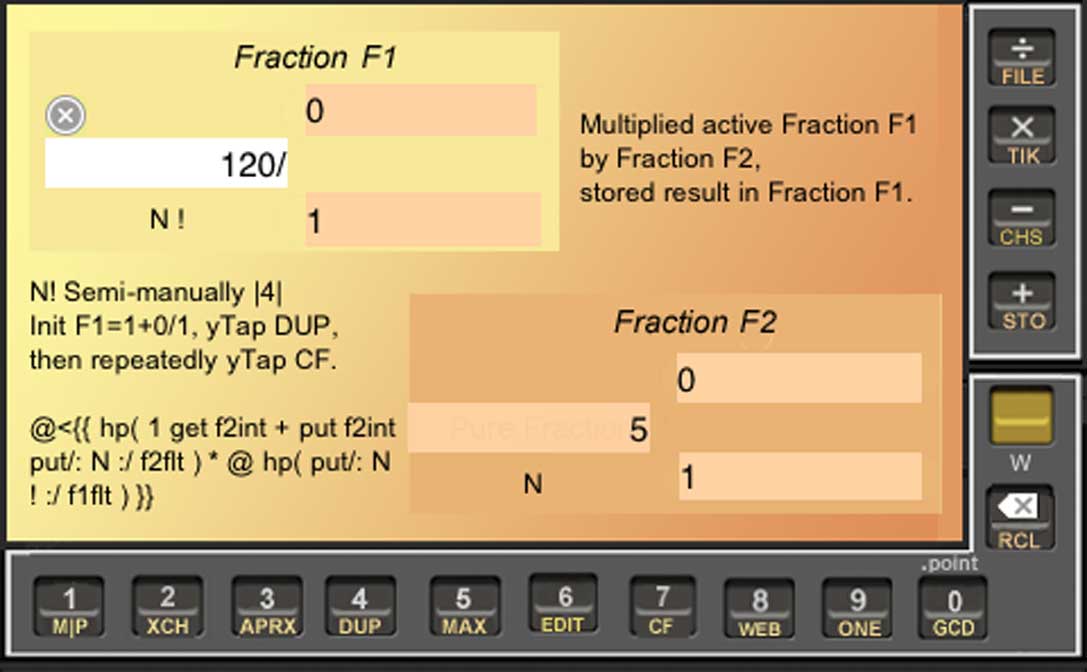
Another example where separate access to Fcells is useful is the following cf bracket for computing the factorial of a small integer:
@<{{
get f2int 1 + put f2int
put/: N :/ f2flt )
*
hp( put/: N ! :/
@ }}
If you initialize F1=1+0/1 and F2=0+0/1, then yTap CF five times, you get the following screen showing 5! = 120:
Another @-loop example, to help clarify order of execution of CF brackets when multiple CF program-brackets are in the same frrrNote:
123 @-Loop Demo
<{{ F1num clr 1 2 3 hp( 0 sto 1
) }}
@{{ hp( rcl 1 1 + dupx sto 1
put f2num put/- second -/
f1num ) }}
@<{{ hp( rcl 1 1 + dupx sto 1
put f1num put/- first -/ f2num
) @ }}
>|41|
|
Try it. Put the above program into frrrNote (either type it in, or use iPhone's Copy/Paste to get it from the web into a fresh frrrNote) and Return-to-Frrr. Look at the program to determine what you think will happen when you run it. While YellowKey is in its temporary Green-T state (due to Return-to-Frrr), tap CF to see. F1num contains 123, and the first of the three program brackets no longer has a <enabler. Clearly, that's the bracket that ran. Which program bracket will run the next time you run CF? Test your analysis by running CF again (YellowKeyStatus is still Green-T, so just tap CF to do it). F2num now contains 'first'. Q: Which function-bracket put that there? A: The third, with its 'put/- first -/ f2num' command. Q: Why did the third bracket run before the second? A: For the same reason the first bracket didn't run again: They had no <enabler and the third one did. Q: The third bracket only had one <enabler; why does it now still have an <enabler? A:It doesn't still have an <enabler; it has a new <enabler—and so does the second bracket—put there by the inside-@ command which executed when the third bracket ran. What will happen if we tap CF again? Did you figure it out? Then try it. We didn't tap Y first and F1num is the active Fcell, so you might expect F1num to now contain 7 or 1237. But it now contains 'second'. Only the second bracket with its 'put/- second -/ f1num' command could have done that. Q: Why did CF run instead of the digit 7 being put into F1num? A: Because the YellowState was Green-T, not White-W, and CF is one of the three special yellowFunctions that don't need Y to be tapped when Green-T is up. Q: Why did the second bracket run instead of the first? A: Because the first had no <enabler whereas the second's <enabler had been replenished as part of an @-loop. Note that the first racket still has no <enabler and, since it ran, the second function-bracket again has no <enabler. So the third bracket is next-in-line to run. From now on, as the members of the @-loop, the second and third brackets take turns running whenever you tap CF. Q: Have you figured out the source of the increasing numbers that alternate with the words 'first' and 'second' in the Fnums? I'll leave it for you to answer. |
|
Background Topic: RPN "Reverse Polish Notation" is all about the order you name numbers and operations when writing arithmetic. The name sounds sophisticated and scary to some people at first, but in practice it's very nice to use. What most people normally use would sound scary too, if schools told you what it's called before telling you how to do it: "In-Fix Notation". See what I mean? There are three notations:
The great thing about RPN is how it eliminates calculation ambiguities that plague the other two notations, such as: What is the result of 7 – 4 * 2 using infix calculation? Is it –1 or is it 6? In-fix processors resort to two artifices to resolve such ambiguities: the hard-to-remember notion of "operator binding precedence" in which *mul has higher precedence than –subtract. In the example, *mul is bound to the 4 more tightly than –subtract is bound to the 4, so 7 – 4 * 2 would be 7 – 8. This notion is augmented with user-provided parentheses to override the natural precedence (or overcome the ok-which-is-it confusion) when necessary. Sometimes the whole expression must be rearranged to contrive the result you want. Thus, presented with 7 – 4 * 3 the in-fix processor multiply 3 by 4, and that result would be subtracted from 7 to get –5. To get the other result you would need to override the natural operator precedence by using parentheses, viz. (7 – 4) * 3 would do 7 – 4 first, to get 3; then do 3 * 3 to get 9. Does that In-Fix approach stll sound simple? I don't think so. We do it just because it's what we first got taught in school. RPN handles the problem this way: It treats data (7,4,2) and operators (–,*) as a simple stream; data items get "pushed onto the stack" one by one as they're received (like dishes onto a steaming stack in a cafeteria); when the next operator comes along in the stream, it "pulls" the data it needs off the top of the stack, however many data items it needs (the common +,–,*, and / operators each needs two, CHS change-sign needs one, and so forth); combines the data as the operator's nature requires; and pushes the result onto the stack—to be treated as data by future operations when they come along in the stream. So. To get In-Fix's 7 – (4 * 3) = –5 result, RPN could use
To get (7 – 4) * 3 = 9, RPN could do 7 4 – 3 *
Note that RPN needs no parentheses or hard-to-interpret precedence rules. It's a simple first-come first-served cafeteria. |
|
Info Topic: hp( hp( operates in frrrNotes within the standard {{...}} CF bracket in the format hp(...). That is, it has its own sub-bracket: The opening brace, an ordinary left parenthesis, is built right into the hp( keyword with no intervening space. The closing brace is an ordinary right parenthesis. Within that bracket, the keywords, all private to hp(, are presented in Reverse-Polish notation—which means that numeric operands are listed first, followed by the operations that need them. For example, to subtract 3 from 22 you could edit the following into frrrNote:
Or, to subtract 3 from the denominator of fraction F1—a kind of thing that might be more useful while being awkward to do in Frrraction itself: The sequence of stacks the first of these would produce is:
Assuming that the fraction cell F1den started out containing 22, the second CF bracket would produce the same sequence of stacks as the first. Operation of the stack is automatic. The only times you need to think about it are when you want to get it to show you some intermediate results that would normally evaporate in the normal course of a computation. For such cases, here's how it works: Called a FILO stack (First-In, Last-Out) the stack owns private operations called "push" and "pull". When an operation produces a result, that value gets pushed onto the stack; a chain reaction pushes the older stack entries down by one position: discards the current contents of T (there being no place for it to go), Z moves down into T, Y moves down into Z, and the new value loads into the newly vacated X-position at the top. When an operation needs an operand value, it pulls it from the top of stack: this retrieves the X-value, lets the old Y float up to replace it, the old Z floats up to replace the old Y, the old T value floats up as the new Z and (what doesn't work with plates in the cafeteria) also leaves the old T in place as a copy. The DUPx and XCHxy operations give a modicum of control over the stack contents, and the hp( operation whose keyword is '=' prints the current contents of the stack in the frrrNote.
|
The CF Bracket facility exposes a slowly growing collection of specialized frrrApplets. Those in support of "Modular Square Roots" have their own section later in this chapter of the Frrraction Guide. Others are listed here.
| keyword | action |
|---|---|
| Classifies an integer as prime or composite. Setup: m in active cell Fcell Action: Fflt announces "Fcell is (or is not) prime" | |
| Raises x to the integer power n Setup: F=n+x/1 where F is the active fraction Action: F becomes r+x/1 where r is the 32-bit nth power of x. The 64-bit r is shown in frrrNote. | |
| Computes the nth power of x (mod p) Setup: activeF=n+x/p. n,x,p all >0; p prime. Action: F becomes r+x/p where r is the nth power of x (mod p). |
|
| Raises the modular complex number z=x+v·y to the power n modulo prime p. w=v^2 is the QNR square of the imaginary carrier v. Setup: F1=n+x/p, F2=w+y/p. Action: The fractions become F1=n+A/p, F2=w+B/p where z^n = A+B·v (mod p). |
|
iMul | Adds or multiplies the "mate"( of the active Fcell) in the inactive fraction to the active Fcell. Setup: x in active Fcell, y in "the mate of the active Fcell" e.g. x in F2den, y in F1den Action: 32-bit result y <op> x → x. 64-bit result is shown in frrrNote, e.g. x=pMAX in active F2den, y=7 in F1den, <{{ iAdd }} in frrrNote; -2,147,483,642 → F2den, 2,147,483,654 is shown in frrrNote. Confused? see Frrraction's huge numbers. |
mn! | mn! and n!Modm are synonyms. They compute n factorial (mod m) Setup: activeF = 0+n/m Action: activeF = n!(mod m) + n/m Note: If you use pMAX for m, the result is the normal n! for 0 ≤ n ≤ 12. For n=13 and beyond, n! would cause 32-bit overflow (while n!Modm does not, of course). 2nd line of Action |
| summary Setup: Action: more |
This is some really fun stuff! (in my humble opinion). If you can find a way to interpret the numbers in a Continued Fraction as letters of the alphabet, then the Continued Fraction becomes a message. And if you convert that Continued Fraction into an ordinary stacked fraction, then the message is quite nicely disguised--especially to people who think numbers are just numbers!
Galen and I have been working with one way to interpret numbers as letters. We call it the simple alphaNum code: Replace A by 1, B by 2, ... , and Z by 26. For better communication we extended the simple alphaNum code to include a number for a blank space, a period, and a question mark. We use 32 for space, 46 for . and 63 for ?.
That's all there is to it. Now [0;23,15,23,46] or 1/(23 + 1/(15 + 1/(23 + 1/46))) or 15931/367472 all contain the coded message "WOW." Cool, eh?
After you catch on, you can begin to let Frrraction do the heavy numeric lifting for you: Put the CF command <[0;23,15,23,46] into frrrNotes (not forgetting the command arrow '<') and CF will put 15931/367472 into the active fraction. Notice that CF removes the Command Arrow to let you know it finished the job. Or go the other way: Put 15931/367472 into the active fraction and an empty square bracket [] into frrrNotes and let CF fill the empty bracket for you, creating the loaded bracket [0;23,15,23,46].
There are two things to avoid:
A typical long message: 16057/16558 28/451 69865/75672 2932/41465 362/1829 1663/1894. The first way I divided it into codewords, two of the codewords ended with A. In each case I just moved the A to the beginning of the next codeword. Those two five-letter codewords didn't cause overflow to occur so there was no other problem.
When you get tired of counting letters of the alphabet to get from messages to numbers, here is Frrraction to the rescue.
The CF Command that converts simpleAlpha to a normal Continued Fraction is: <[@ followed by the alphabetic letters of a codeword and the closing square bracket ]. Use NOTE to put that into frrrNotes, then employ the CF function. Bingo. frrrNotes then contain the bracket form of the continued fraction.
For example, if you put <[@SHOW] into frrrNotes, then the CF function will replace it by [@SHOW] <[0;19,8,15,23,]. So frrrNotes would then contain a new CF Command, ready for the CF function to put the numeric continued fraction, which encodes the alphaNum SHOW message, into the active Fraction.
Frrraction can also go the other way: it can decode a stacked fraction which happens to be the alphaNum-encoded form of a text message: The CF Command in frrrNotes is just [@] and Frrraction's CF function fills the empty bracket with the decoded form of the active fraction.
For example, if the active fraction contains 2791/53375 and [@] is in frrrNotes then the CF function will replace [@] by [@SHOW]. If the active fraction was just a number, not an alphaNum-encoded message, what you would most likely get from CF is [@~~~~] because the tilde character ~ is what the CF function uses when it doesn't recognize a number as an alphaNum-encoded character.
The next step in Frrraction's Secret Message Codec facility is to use the much more powerful ASCII code instead of the overly simple alphaNum code. The only difference in operation is that the alphaASCII flag is the tilde character ~ rather than alphaNum's @ character. Thus, <[~Wow 012!] converts to [0;87,111,119,32,48,49,50,33,]. The stacked form of that particular numeric continued fraction happens to be so huge it generates an Overflow in Frrraction. The three-to-five character codeword limit applies to ASCII as well as to alphaNum. Breaking it up into two four-letter codewords we get [0;87,111,119,32] = 422831/36790106 and [0;48,49,50,33] = 80932/3886387.
ASCII is Page 1 of UTF8 and Unicode, the world's most important standard communication codes, so well worth being a little familiar with. For reference, here is a convenient list of ASCII codes. Good news is: You do not need to actually know ASCII in order to use it in Frrraction.
Decoding an ASCII-encoded stacked fraction is just as easy: Put an empty ASCII-flagged bracket [~] into frrrNotes and the active fraction will be decoded into the empty bracket. For example, if Fraction F2 were active and contained 80932/3886387, the empty bracket would be replaced by F2 = [0;48,49,50,33][~012!] — the numeric continued fraction followed by its ASCII-decoded form.
A final note: The two alpha encodings are mostly incompatible with each other — they share only the space, period, and question mark. I assume that, once you get to the ASCII [~ forms, you won't feel a need to turn back to the simple alphaNum [@ forms.
background
Sometimes you have a fraction whose numbers are too large for the purpose at hand. Frrraction's APRX function provides an easy-to-use solution that you already know about. The CF continued fraction provides a fascinating alternative.
Example: Suppose you want a simpler fraction than 1,010/7,009 but with the same 7-digit decimal value. Putting 1,010/7,009 into Fraction F1 and doing doubleclick-00 puts the decimal form 0.1441004 into F1int. APRX then finds the simpler stack 712/4,941 which has the decimal form 0.14410038, which rounds to exactly match the seven digits of F1int.
Another way to get that result--and the whole point of this CF Example section of the guide--is to use CF continued fractions to find the most efficient fraction that represents any number in the range from 0.14410035 to 0.144100449, i.e. any number that rounds up or truncates down to the given seven digits. Here's how:
|
Try it. Really. Step 1: Put 0.14410035 —the smallest number that rounds up to match 0.1441004—into F1intD and put an empty Continued Fraction bracket [] into frrrNotes, then use the CF function. This replaces the empty CF bracket by F1 = [0;6,1,15,1,1,3,1,3,3,1,...]. Step 2: Put 0.144100449 —the largest number that rounds down or truncates to match 0.1441004—into F1intD, put another empty bracket [] into frrrNotes, and apply CF again. This replaces the empty bracket by [0;6,1,15,1,1,3,1,6,2,1,...]. Step 3: Make a new bracket by copying the previous two as far as they agree, producing [0;6,1,15,1,1,3,1,]. At the next entry, the two brackets disagree: the smaller has a 3, the larger has a 6. Complete your copy by using 1 plus the smaller, viz. 4, so it reads [0;6,1,15,1,1,3,1,4]. Convert that bracket into a command bracket by putting a left-angle-bracket in front of it, to obtain: <[0;6,1,15,1,1,3,1,4]. Step 4: Exit the frrrNotes editor, tap any F2-cell, and use the CF function. It will convert your command bracket into the stack 712/4,941. Exactly the same as APRX got (APRX took less work on your part, but a lot more on the computer's part!). |
Fig. APRX2 summarizes the example. The frrrNotes have been edited to include all three steps in one screen. Using NOTE, I simply typed the lines "Best Approximation Example" and "1010/7009 = 0.1441004" after doubleclick-00 gave me the decimal value. The lines "F1 = ... = 0.144..." were produced from empty brackets by the CF-command in Step 1 and Step 2. The line "Lesser+1..." shows what's left of the CF-command-bracket <[0;6,1,15,1,1,3,1,4] after Step 3 collapsed it into F2.
|
Try it. Really. For a second example, suppose you would be satisfied with a 4-digit approximation 0.1441 for that same fraction used above. Then the above steps become:
|
|
Try more: In the above examples we chose intervals to contain precisely all decimals that match (after rounding) a given decimal to a given number of digits. The examples directly generalize to finding the most efficient stack for a number required only to lie within a specified interval—any interval you want. |
This starter reference on best approximations explains in more detail.
↑ to Frrr104 MenuFrrraction offers a constellation of CF functions that address square roots in various forms:
|
Background of mSqrt: mSqrt is unsophisticated, and can be quite time-consuming when p is larger than a few million: It uses a brute force search method, checking all residues one at a time to see whether its square, reduced modulo p, is congruent to x. It was not Frrraction's first nor least-sophisticated modular square root solution, however. That one was based on the fact that √x mod p is always simply the integer square root of an integer perfect square that can be expressed in the form: k·p + x for some positive integer k. The method tried k-values one at a time, looking for the smallest for which k·p + x was an integer perfect square—which it recognized by its being the sum of the first j odd integers; having found such a value for k, voila!: j was √x. This approach works fine if the sought-after value of k is small, but bogs down otherwise. An example where k is too large to find comfortably by simple calculator operation is √7 mod 4567. In this case one finds that 111·4057 + 7 is an integer perfect square, and can easilty proceed from there to the desired square root—but nobody's patience would tolerate the manula search through 111 values of k in order to reach that point. |
|
TryIt: One of 6 or 7 has a square root modulo 4,567. Determine which one it is, and find the square root. Hint: It's not easy to do without software help. |